Zusammengesetzte Ereignisse
Die Frage nach dem Ausgang eines Zufallsexperiments kann aus einzelnen Teilfragen zusammengesetzt sein,
die mit und bzw. oder verknüpft sind.
Natürlich kann man auch nach der Wahrscheinlichkeit fragen, dass ein Ereignis nicht eintritt.
Es seien A und B zwei Ereignisse, dann bedeutet …
- A ∪ B (gelesen "A oder B" oder "A vereinigt B"), dass A oder B eintritt, wobei das oder nicht im Sinne von "entweder oder" verstanden werden darf!
- A ∩ B (gelesen "A und B" oder "A Schnitt B"), dass A und B eintritt.
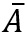(gelesen "A quer" oder "nicht A"), dass A nicht eintritt.
Wenn zwei Ereignisse A und B sich "überlappen", d.h. wenn sie geimeinsame Elemente haben, dann kann man die Einzelwahrscheinlichkeiten nicht einfach zusammenzählen, denn andernfalls würden wir die gemeinsamen Elemente doppelt berücksichtigen. Das heißt, dass wir in dem Fall die Schnittmenge einmal wieder abziehen müssen. Diese Vorgehensweise wird im "Großen Additionssatz" formal geklärt.
Großer Additionssatz: Wahrscheinlichkeit von "A oder B"
Beachte: Hier ist "oder" nicht als "entweder oder" zu verstehen!
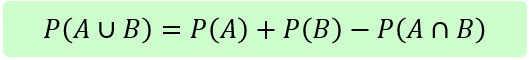
(Das Zeichen {} steht für die leere Menge).
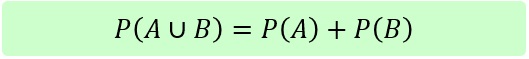
Wie groß ist die Wahrscheinlichkeit bei einmaligem Ziehen, aus einer Urne mit zehn durchnummerierten Kugeln (1 bis 10) eine Kugel mit einer geraden Zahl oder mit einer Primzahl zu ziehen?
Lösungsweg 1 (direkt)
A = "gerade Zahl" = {2,4,6,8,10}, B = "Primzahl" = {2,3,5,7}.
Es folgt "A oder B" = A∪B = {2,3,4,5,6,7,8,10}, also P(A∪B)=|A∪B|/|S|=8/10=0,8=80%.
Lösungsweg 2 (Großer Additionssatz):
Mit A und B wie oben ist A∩B={2}. Damit ist P(A)=5/10, P(B)=4/10 und P(A∩B)=1/10, also P(A∪B)=P(A)+P(B)-P(A∩B)=5/10+4/10-1/10=8/10=0,8=80%
Intuitive aber FALSCHE Lösung zum Vergleich:
Hätten wir hier einfach die Einzelwahrscheinlichkeiten addiert, so hätten wir die Zahl 2 doppelt verwendet. Damit wäre wie vorher P(A)=5/10 und P(B)=4/10 also P(A∪B)=P(A)+P(B)=90%, was falsch ist. Wir müssen also tatsächlich gemäß dem großen Additionssatz die gemeinsamen Elemente, also die Schnittmenge, wieder abziehen! Die Einzelwahrscheinlichkeiten können nur zusammengezählt werden, wenn es keine Schnittmenge gibt! Wahrscheinlichkeit von A und B
Sofern die Ereignisse A und B unabhängig voneinander sind, gilt für die Wahrscheinlichkeit von "A und B" folgendes:
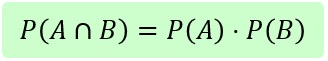
Wenn Sie festgestellt haben, dass die Ereignisse völlig unabhängig voneinander sind, d.h. dass sie sich nicht gegenseitig beeinflussen, dann können Sie die Wahrscheinlichkeit einfach mit obiger Formel bestimmen.
Rechenbeispiel 2
Von 22 Kindern einer Schulklasse mögen 18 Kinder Schokoladeneis und 17 Kinder Vanilleeis. 2 Kinder mögen weder das eine noch das andere. Wie groß ist die Wahrscheinlichkeit bei zufälliger Auswahl, ein Kind zu wählen, das Schokoladeneis und Vanilleeis mag?
Lösung mit einem Venn-Diagramm
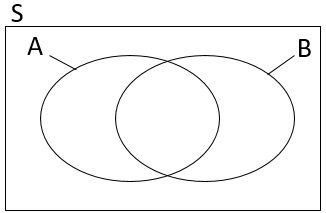
Hier besteht die Schwierigkeit, die Anzahl der Kinder in der Schnittmenge zu bestimmen. Am Einfachsten verdeutlicht man sich die Situation in einem Venn-Diagramm. Der Kasten in der Abbildung rechts ist die Menge aller Schüler, also der Stichprobenraum S. A ist die Menge der Kinder, die Schokoladeneis mögen. B die Menge der Kinder, die Vanilleeis mögen. Jetzt müssen wir nur noch die korrekten Anzahlen für jeden Bereich ermitteln.
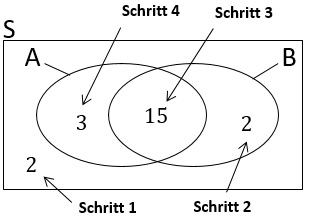
Schritt 1: 2 Kinder mögen weder Schokoladeneis noch Vanilleeis, d.h. sie liegen außerhalb von A und B.
Schritt 2: Es bleiben noch 20 Kinder für beide Ovale, also für A∪B. Da A 18 Kinder enthält, bleiben für den Teil von B außerhalb von A noch 2 Kinder übrig.
Schritt 3: B enthält 17 Kinder, aber 2 davon gehören nicht zu A (das wissen wir aus Schritt 2). Also bleiben 15 Kinder für die Schnittmenge A∩B.
Schritt 4: A enthält 18 Kinder und die Schnittmenge umfasst 15 Kinder. Also bleiben für den "Rest2 von A noch 3 Kinder.&xnbsp;
Damit haben wir nun alle Angaben vervollständigt! Es folgt:
P(A∩B)=|A∩B|/|S| =15/22≈0,682=68,2%
Ergebnis: Mit einer Wahrscheinlichkeit von 68,2% wählt man ein Kind, das sowohl Schokoladeneis als auch Vanilleeis mag.Wahrscheinlichkeit von "Nicht A"
Rechenbeispiel 3
Wie groß ist die Wahrscheinlichkeit, bei gleichzeitigem Würfeln mit zwei Würfeln, keinen Pasch (zweimal dieselbe Zahl) zu bekommen?
Lösung (mit Gegenereignis)
Es gibt 6 Möglichkeiten, bei einem Wurf mit zwei Würfeln, einen Pasch (= zwei gleiche Zahlen) zu würfeln. Insgesamt gibt es 36 mögliche Kombinationen. Wenn wir das Ereignis "Pasch" mit A bezeichnen, dann bedeutet
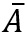"kein Pasch".
Es folgt: P(A)=6/36=1/6 und somit
P()=
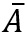1-P(A)=1-1/6=5/6≈0,833=83,3%.
| Downloads |
PowerPoint